Pamraat Parmar

This project is a final assimilation of all the aspects of autonomous robotics. The robot is dropped in partially known environment (such as bounds and location of certain walls) without localization. The robot uses the partial information of the environment, localizes itself, generates Probabilistic RoadMap (PRM) to next goal, and discovers rest of the map while visiting all the goals.

Github Link: https://github.com/pamraat/AlmightyRobot
Notes: To operate this code, you'll need a valid MATLAB license and iRobotCreateSimulator toolbox which can be downloaded from here.

The robot uses Particle Filter with depth data from Real Sense camera and plans it motion using low discrepancy based PRM. The mapping is grid based. All the walls are thick, and are accounted for in robot algorithm. The video shows performance of robot when it was intiated from a certain location.

The post processed data collected after the run is shown in the figure below. The overhead localization shown in green was not provided to the robot, and the particle filter (particles shown in red) was using depth sensor data only. The trajectory was extremely accurate, while robot managed to visit all the goals. The logic flow chart of the algorithm is shown in the figure below.

This project demonstrates the implementation of multirobot system control called Boids developed by Van Hunter Adams. This control algorithm is inspired by flocking behavior of different living organims in the ecosystem like birds and fishes.

Github Link: https://github.com/pamraat/port-boids
Notes: To operate this code, you'll need a valid MATLAB license.

Boids is an artificial life program that produces startlingly realistic simulations of flocking behavior. Each "boid" follows a very simple set of rules. but they can be summarized as follows:

• Separation: boids move away from other boids that are too close
• Alignment: boids attempt to match the velocities of their neighbors
• Cohesion: boids move toward the center of mass of their neighbors

Each decision rule has an associated parameter, which can tweaked to achieve the required behvaior. Following represents the behavior of flocking in every 4th boid.

This project was developed to localize the robot based on depth camera data and compare with overhead localization and dead reckoning from odometry data. The algorithms robustly handle massive discontinuous, and initialization-sensitivty is low.

Github Link: https://github.com/pamraat/port-localization
Notes: To operate this code, you'll need a valid MATLAB license and iRobotCreateSimulator toolbox which can be downloaded from here.

A localization algorithm based on Particle Filter using depth sensor data for a robot is developed. Particle Filter(PF) performs significantly better than Extended Kalman Filter in localization without requiring to apply sensor data filters. The performance of PF with 500 particles is shown in the figure below.

However, it has to be noted that the number of particles significantly impact quality of localization. For e.g., the particle filter with 20 particles is shown below, which coverges eventually, but takes a while to do so.

These codes used in the simulator were implemented on a real robot. The figure below shows the performance of Particle Filter. Despite the error buildup due to motor slipping, sensing noise, and error instilled due to collision with walls, particles maintain localiation. This operation is ran with 200 particles initialized in the small space in vicinity of real robots.

This project was developed to map an unknown environment based on depth camera data. The algorithm is probabilistic and assigns probability if a given part of grid is a wall or not. The same algorithm is then associated with localization techniques to map the environment and localize the robot with respect to that environment, refered to as Simultaneous Localization and Mappin (SLAM).

Github Link: https://github.com/pamraat/port-mapping
Notes: To operate this code, you'll need a valid MATLAB license and iRobotCreateSimulator toolbox which can be downloaded from here.

The robot is randomly initialized in a map with grid size of 25x25. The video below shows evolution of map as robot moves. The darker the cell, higher probability that they are a wall.

These codes used in the simulator were implemented on a real robot. The figure below shows the map estimated by the robot on a given lab environment.

A localization algorithm based on Extended Kalman Filter (EKF) using depth sensor data for a robot is integrated with mapping algorithm such that location of the obstacle is estimated using EKF as well. A robot is operated in an unknown test environment. The results of this result are shown in the figure below.

The fast SLAM algorithm in which localization is based on Particle Filter (PF) using depth sensor data for a robot is integrated with mapping algorithm such that location of the obstacle is estimated using EKF. A robot is operated in an unknown test environment. The results of this result are shown in the figure below.

This project was a part of a larger umbrella-project of implenting motion planning algorithms. Cellular Decomposition is an algorithm where any given polygonal map is sub divided into convex polygonal space. Each convex polygon is assigned a node on geometric center, midpoint of left edge, and midpoint of right edge.

Github Link: https://github.com/pamraat/port-roadmap
Notes: To operate this code, you'll need a valid MATLAB license and iRobotCreateSimulator toolbox which can be downloaded from here.

The random polygonal environment is provided, and the task is to generate a roadmap for any intial point-goal pair on this map.

Definition of a convex polygon is that two points on the convex polygon can be connected by a straight line fully contained in that polygon. By that definition, if we are able to decompose a non-convex polygonal shape into multiple convex-polygonal shape, we can generate a create a complete roadmap in that space. The image below shows roadmap generated in a random polygon environment.

This project was developed to localize the robot based on depth camera data and compare with overhead localization and dead reckoning from odometry data. The algorithms can handle discontinuous readings, however, robustness depends on initialization.

Github Link: https://github.com/pamraat/port-localization
Notes: To operate this code, you'll need a valid MATLAB license and iRobotCreateSimulator toolbox which can be downloaded from here.

Initially, grid-based localization is set up to lay grounds for Kalman Filter based algorithms. A low resolution grid is used, and the depth sensor data is fed into the algorithm. The result for 10x10 grid is shown below.

This is compared to a high resolution grid, and result is shown below, which conforms better to the expected result.

Next, the same data is fed to Stationary Kalman filter and the next 2 images show results for different initializations. Both results conform to expectations.

A localization algorithm based on Extended Kalman Filter using depth sensor data for a robot is developed. Extended Kalman Filter(EKF) is used instead of Kalman Filter as nonlinear variations in depth measurements based on robot motion are expected along with discontinuities. The performance of EKF is shown in the figure below.

These codes used in the simulator were implemented on a real robot. The figure below shows the performance of Extended Kalman Filter. Clearly, the error buildup is signifcant due to motor slipping, sensing noise, and error instilled during collision with walls. Advanced sensor data filters were used to minimize the localization errors. The reason behind the deviation towards the end of motion is due to malfunctioning filters in wide open space where depth data is highly erroneous.

This project was developed to control the robot actuators, communicate with ground computer, and acquire & analyze sensor data. The algorithms are robust and can handle any unexpected issues in control, communication and sensing.

Github Link: https://github.com/pamraat/port-robot-actuation
Notes: To operate this code, you'll need a valid MATLAB license and iRobotCreateSimulator toolbox which can be downloaded from here.

The robot is a modified roomba controlled with Raspberry Pi 3 Model B. For overhead localization, video camera was used. Moreover, Real Sense Depth camera, bump sensors and odometry sensor was installed on the robot.
In this project, the robot uses feedback linearization to move form its current location to the goal. In the video shown above, robot moves from (0, 0) to (-3, 0) to (0, -3) to (3, 0) to (0, 3). The robot uses bumb sensor to detect collision with walls, backs up, turns 30° counter clockwise and continues moving.

The codes used in the simulator were implemented on a real robot. The figure below describes the actuation error.

The image below shows robot response to feedback linearization for different feedback gain &epsilon, where * represent the points it is attempting to visit.

This project was a part of a larger umbrella-project of implenting motion planning algorithms. Rapidly-Exploring Random Trees (RRT) is an algorithm by which the road-tree rapidly grows till it finds a direct line of sight path towards goal.

Github Link: https://github.com/pamraat/port-roadmap
Notes: To operate this code, you'll need a valid MATLAB license and iRobotCreateSimulator toolbox which can be downloaded from here.

RRT are chance-based algorithms, i.e., it is quite possible that it takes very few computations to converge to otherwise very complicated solution, or it may take significantly large Computational efforts to converge to a relatively simple problem. However, it can be mathematically shown that RRT will always discover a roadmap. The video below shows RRT in action, where blue diamond represent the goal point. Note the intermittent red dashed lines, they represent the tree branches rejected by the algorithm as it must be violating one or more criteria.

The RRTs perform well in real life as well. The performane of an RRT algorithm implemented on a real robot is shown in the figure below. Note that the lines depicted here are thick walls, and RRT algorithm takes into account the thickness.

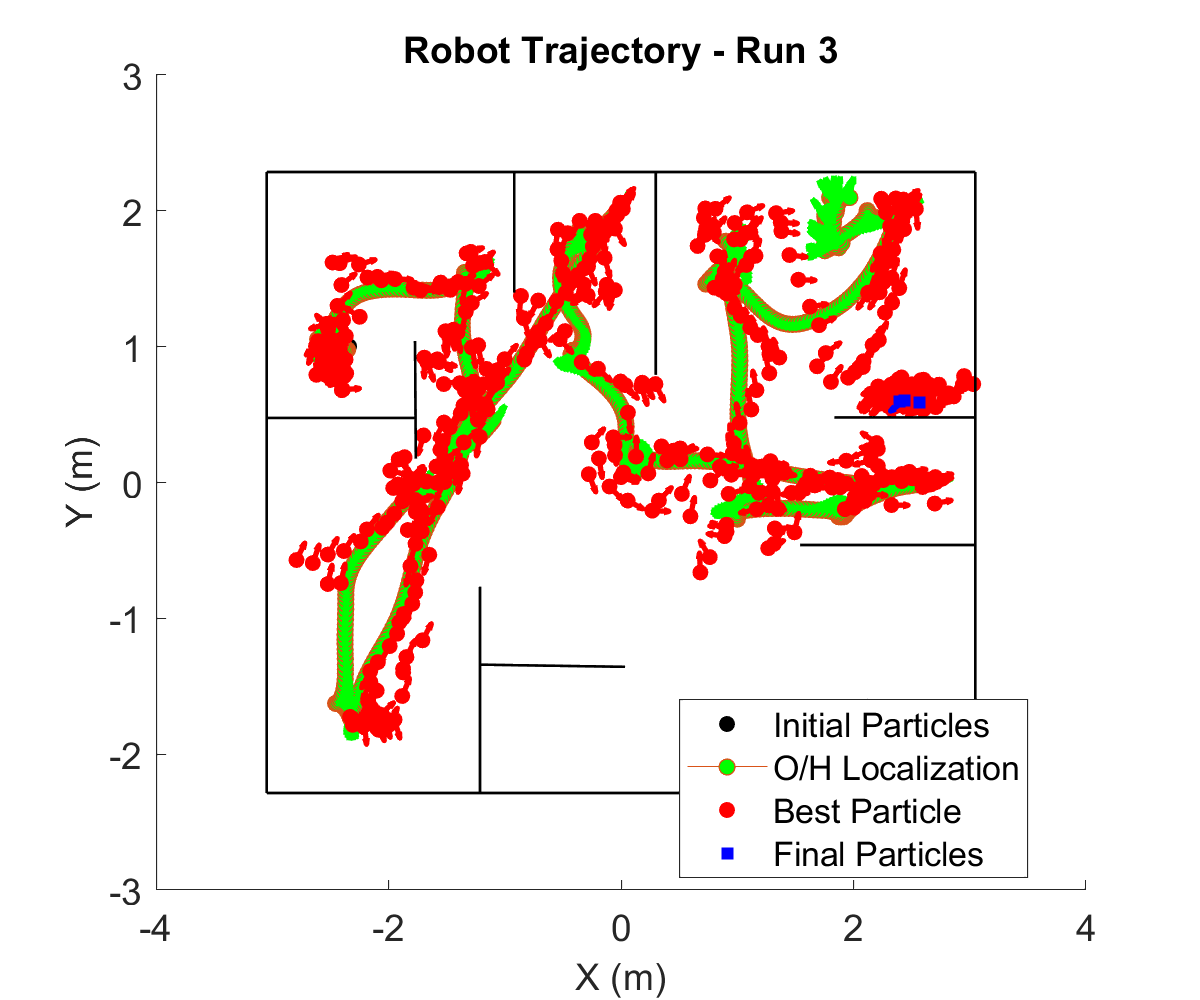
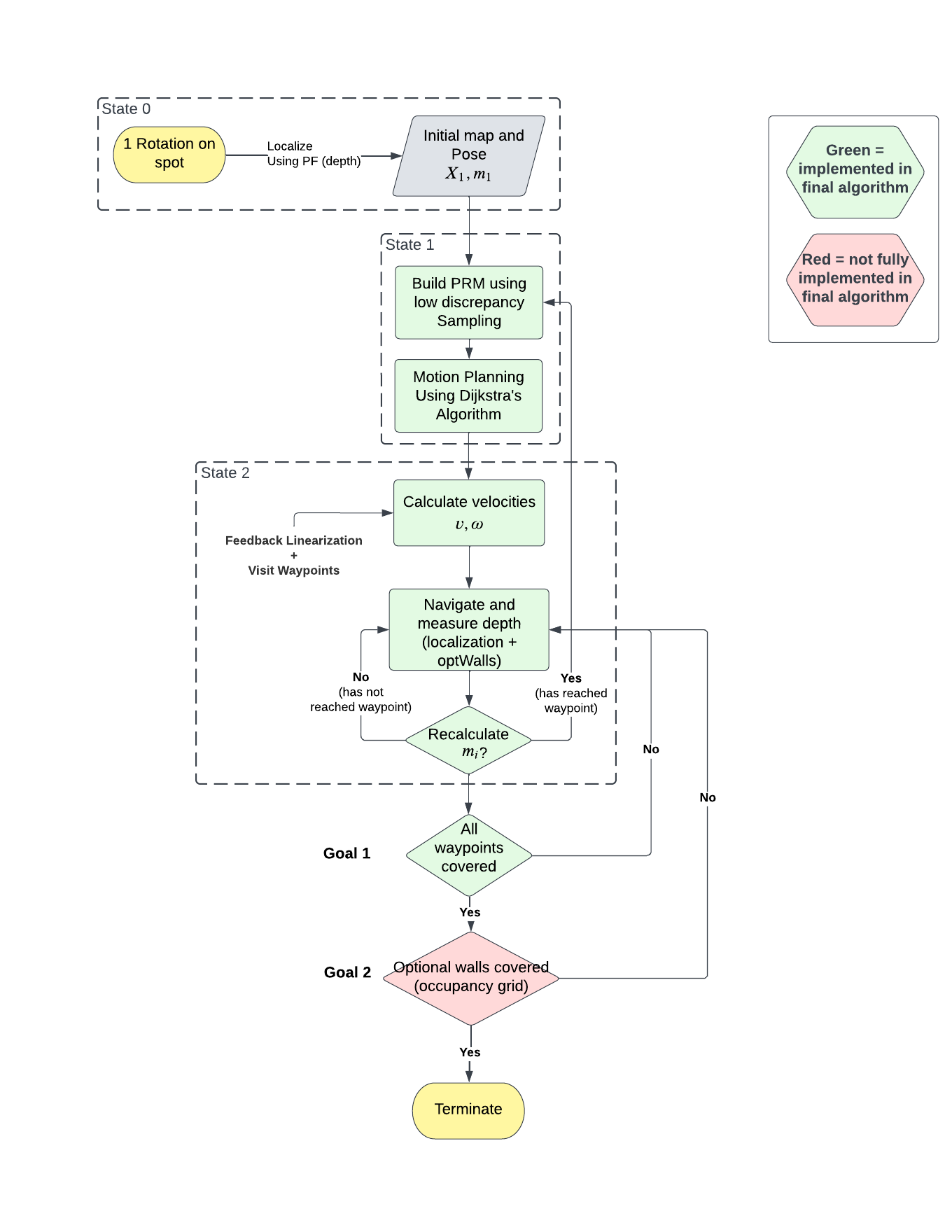
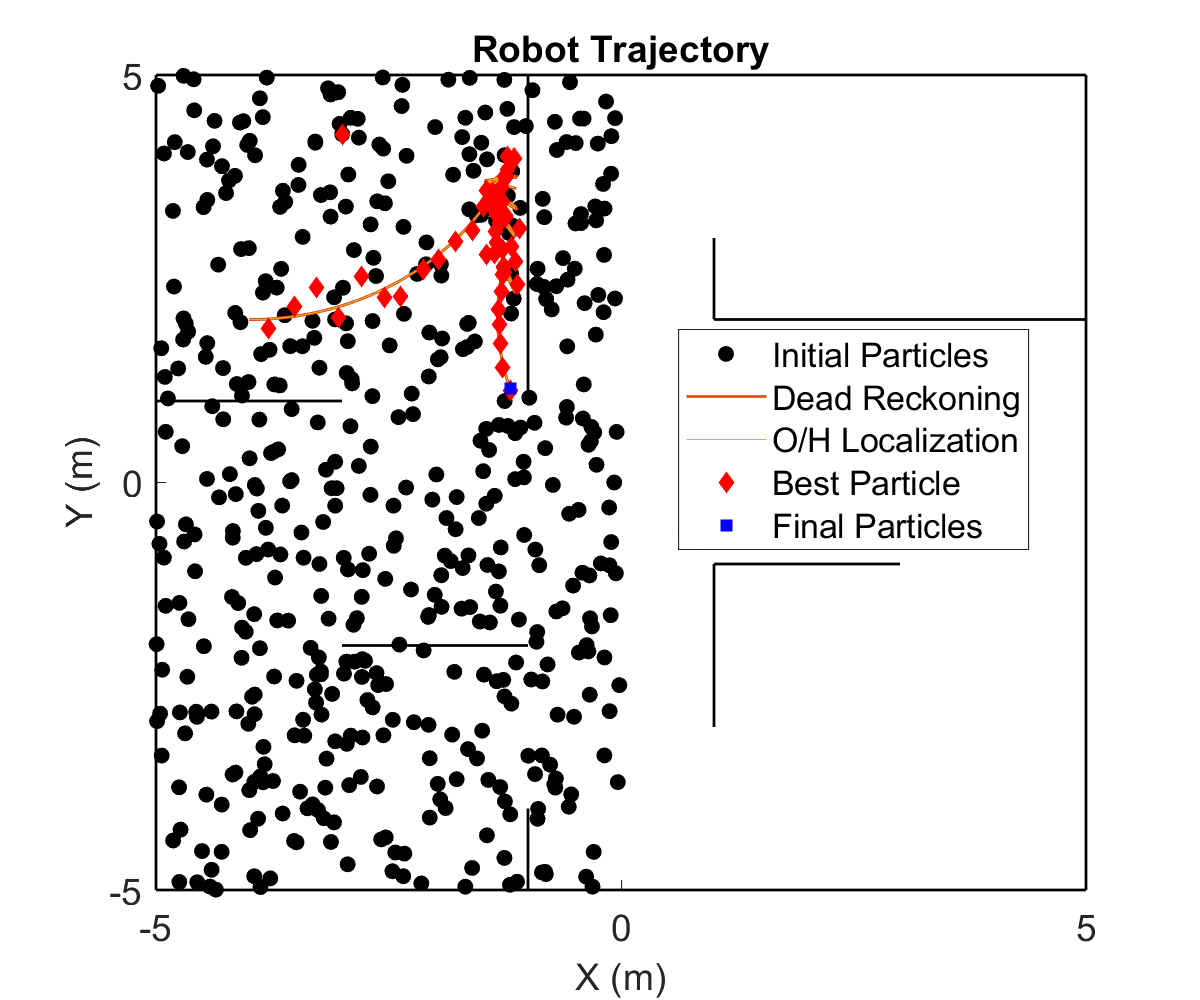
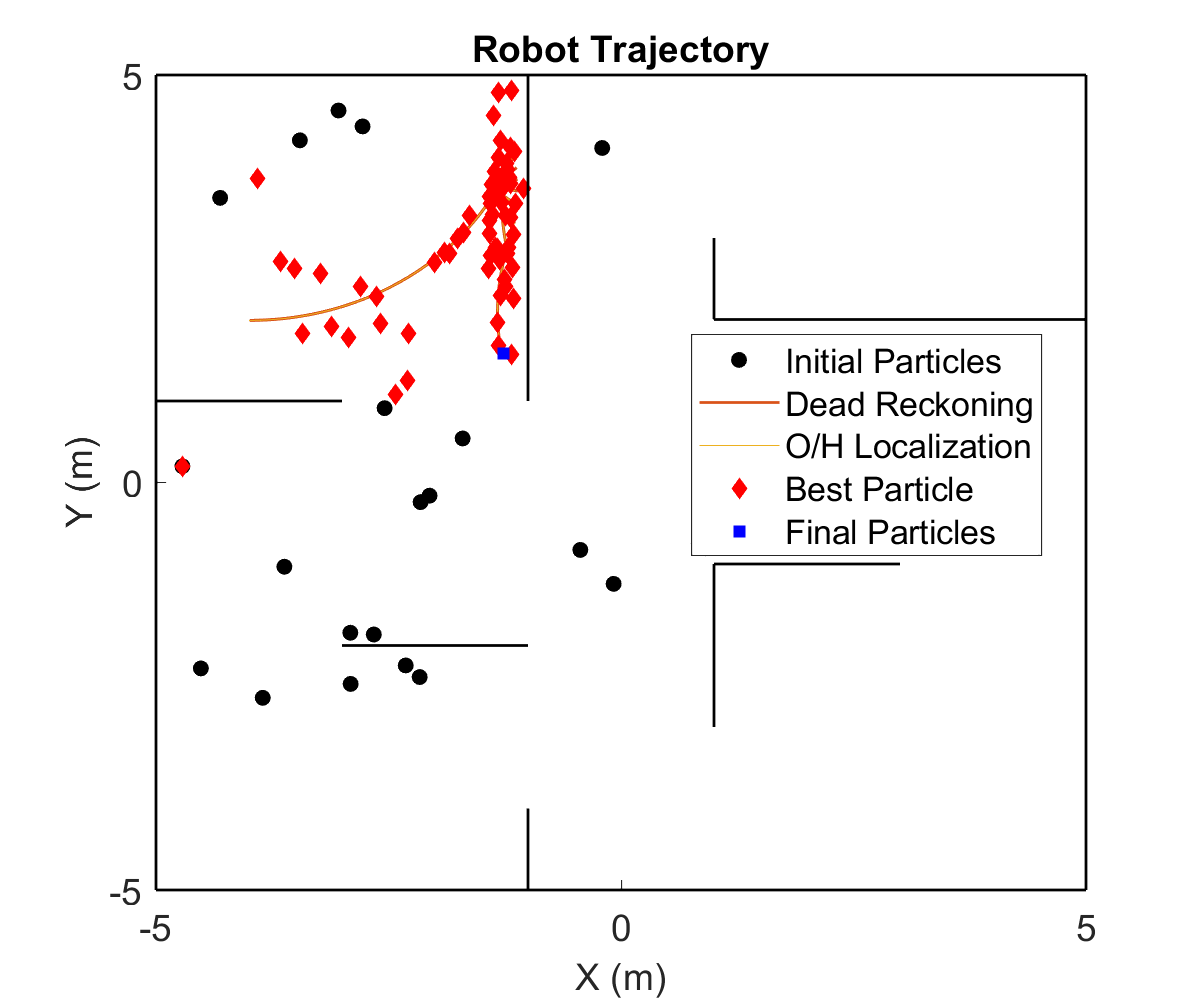
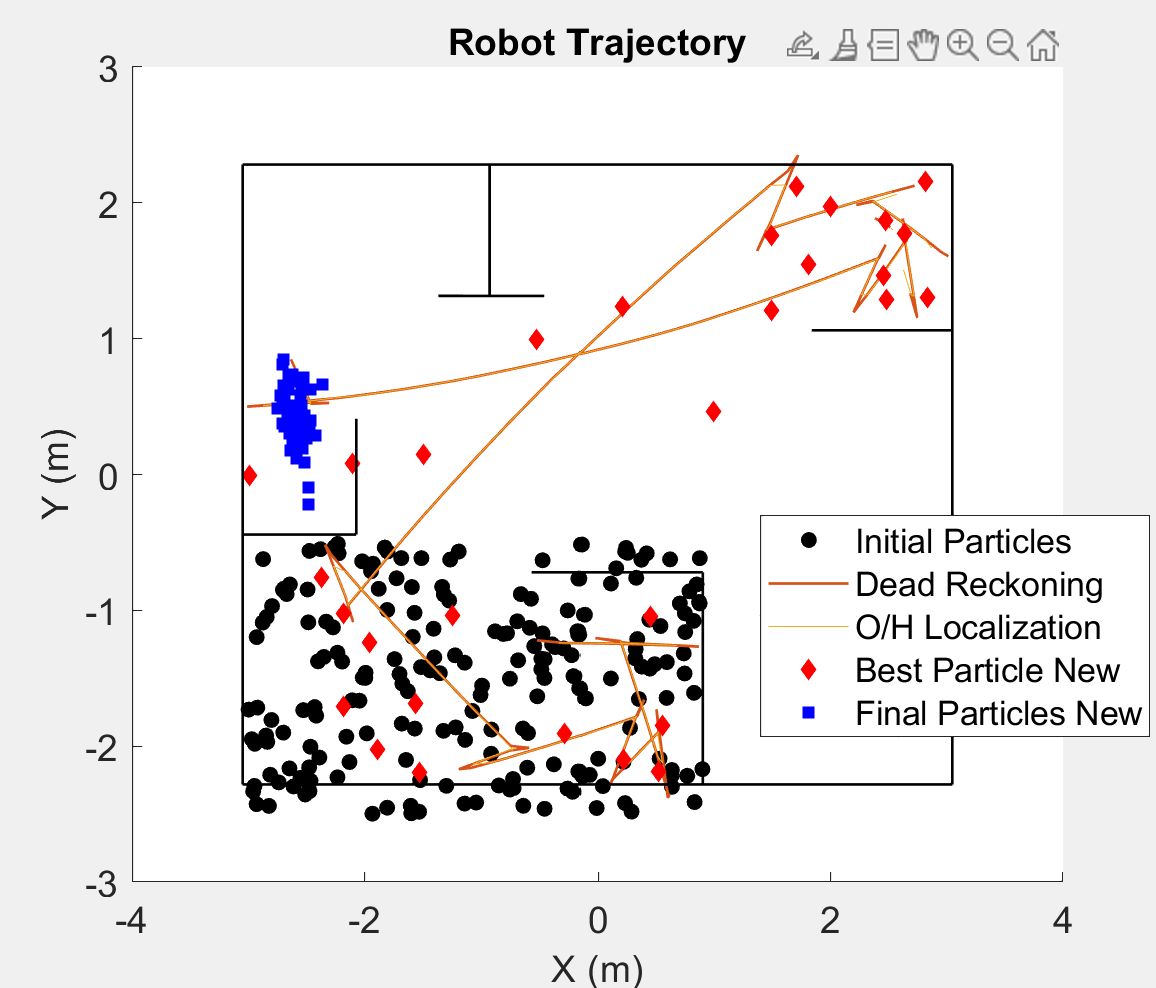
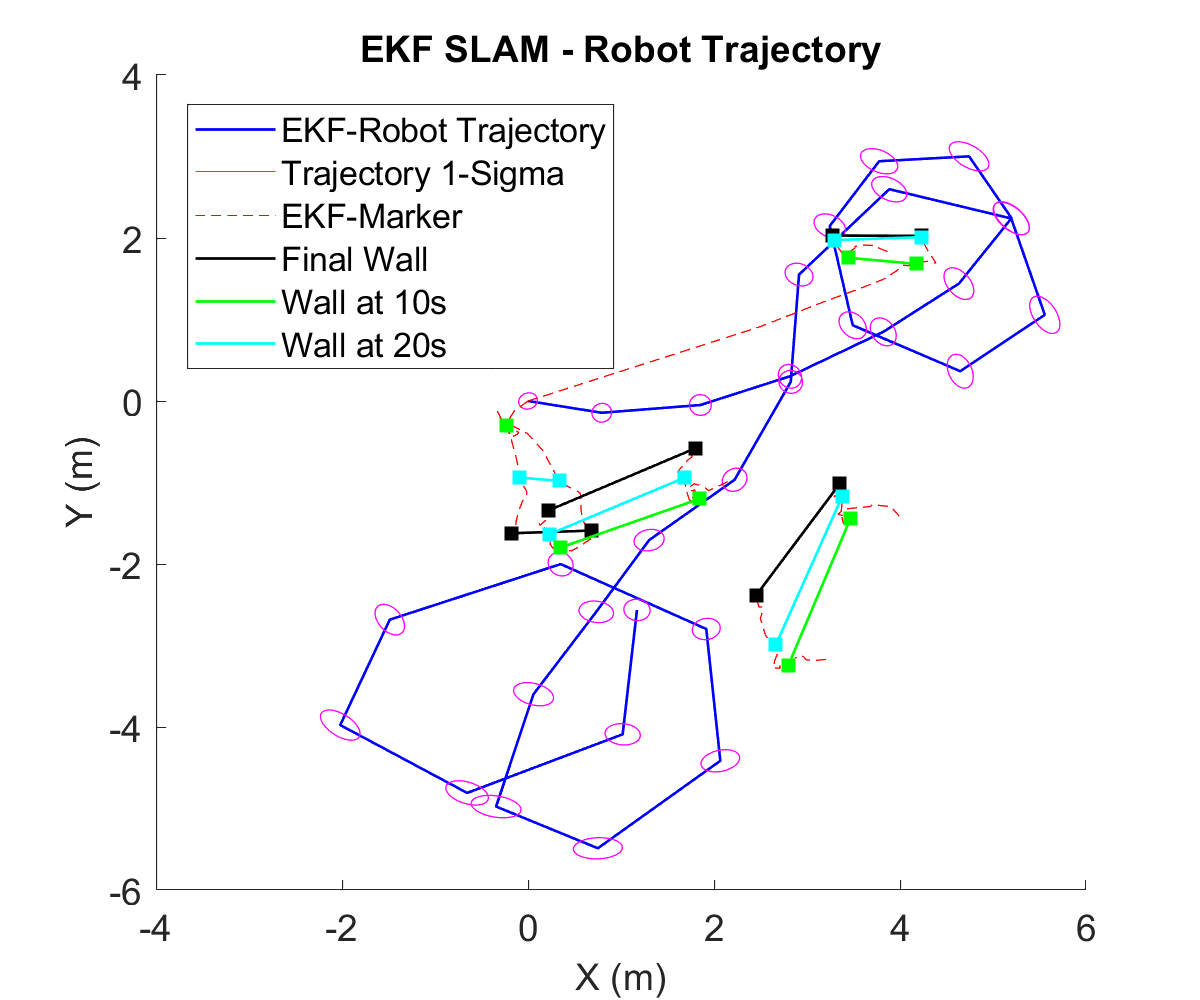
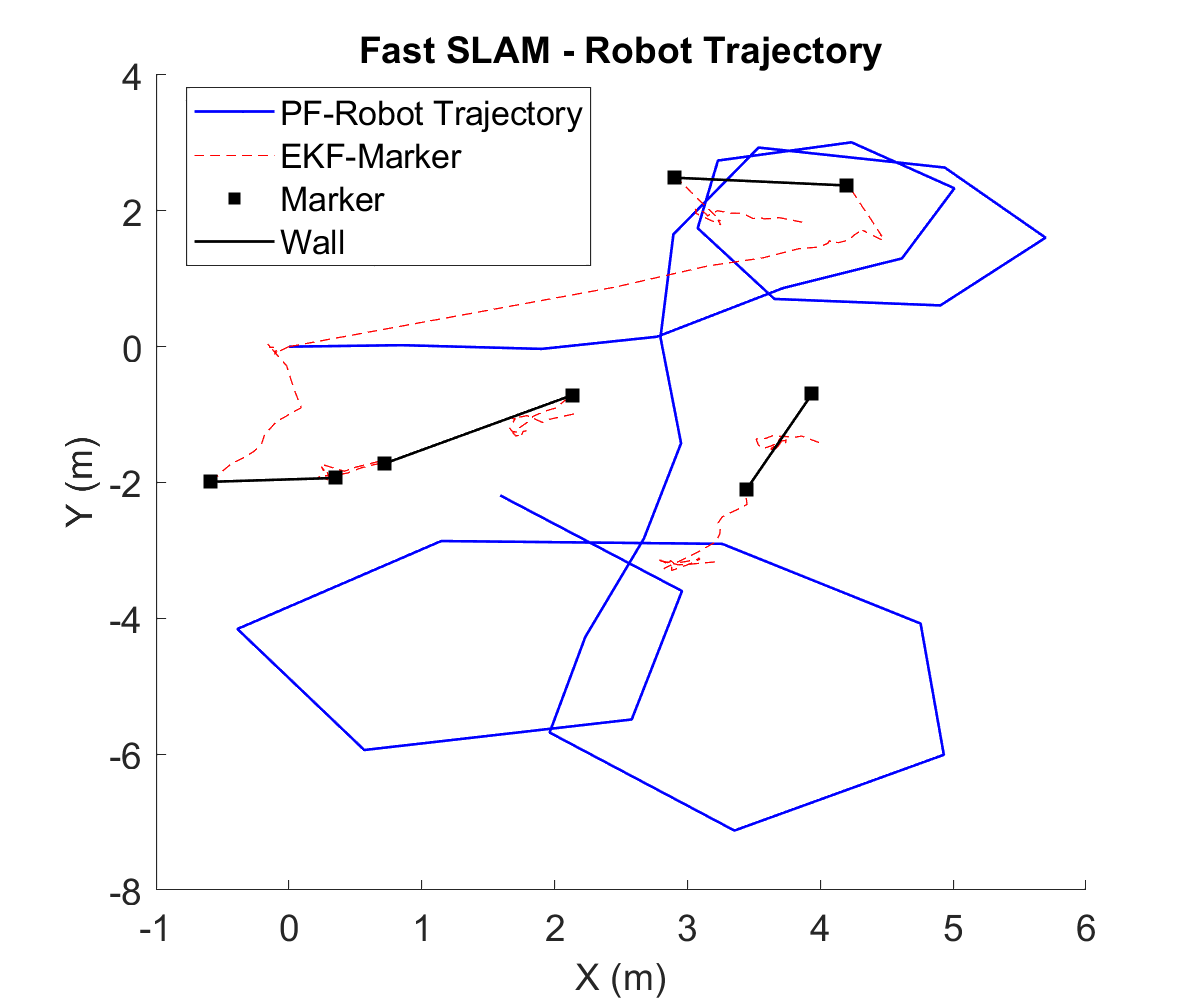
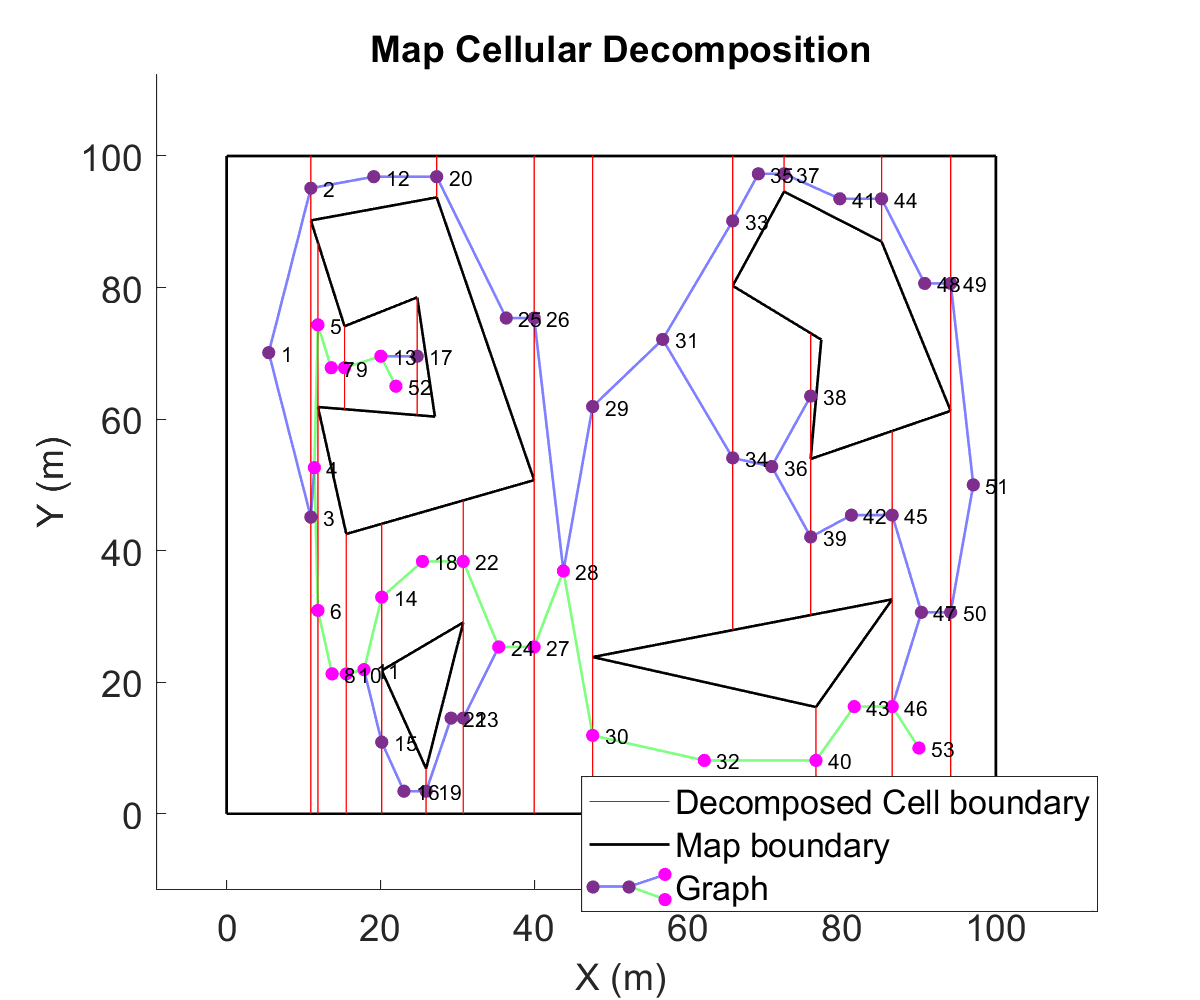
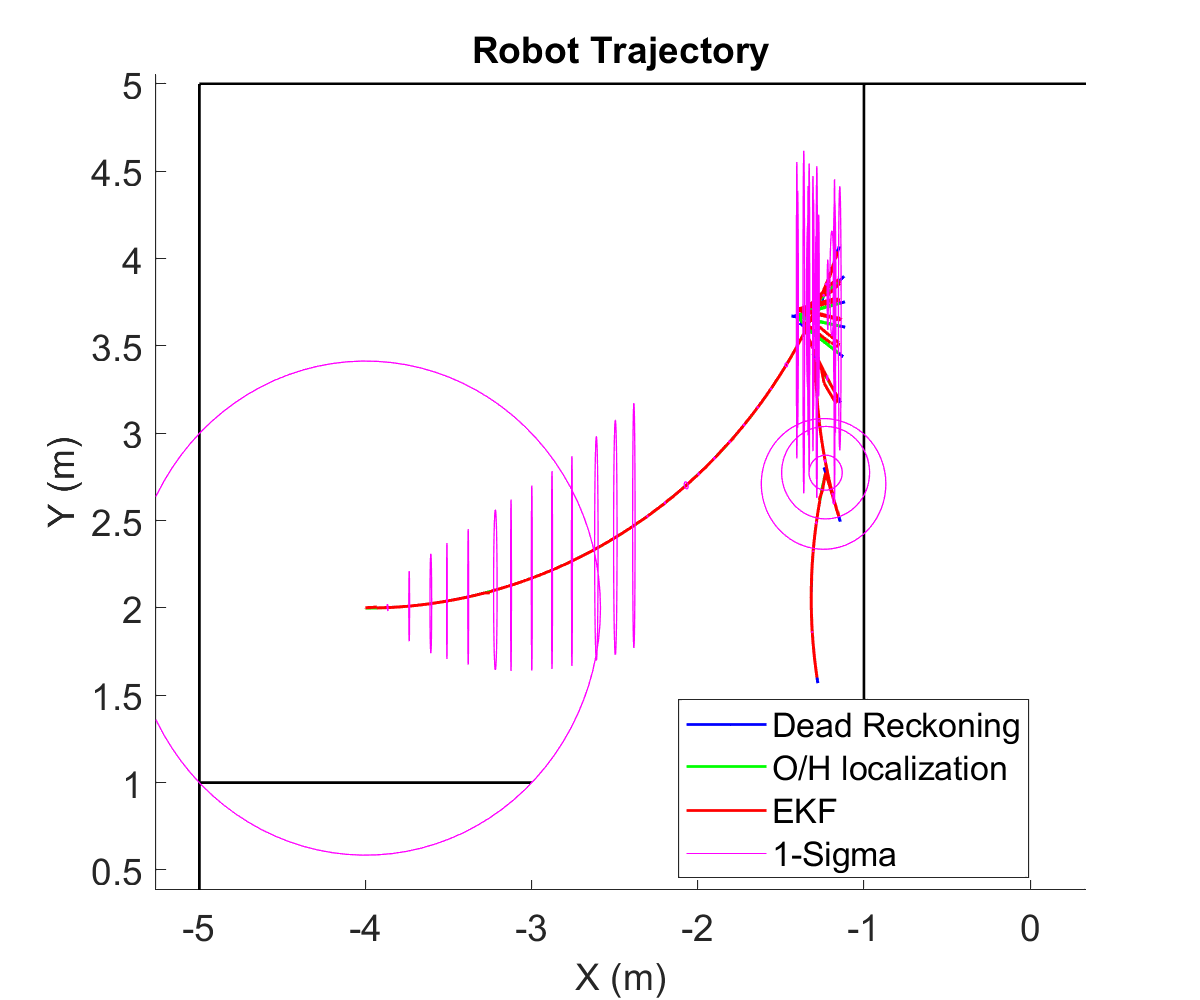
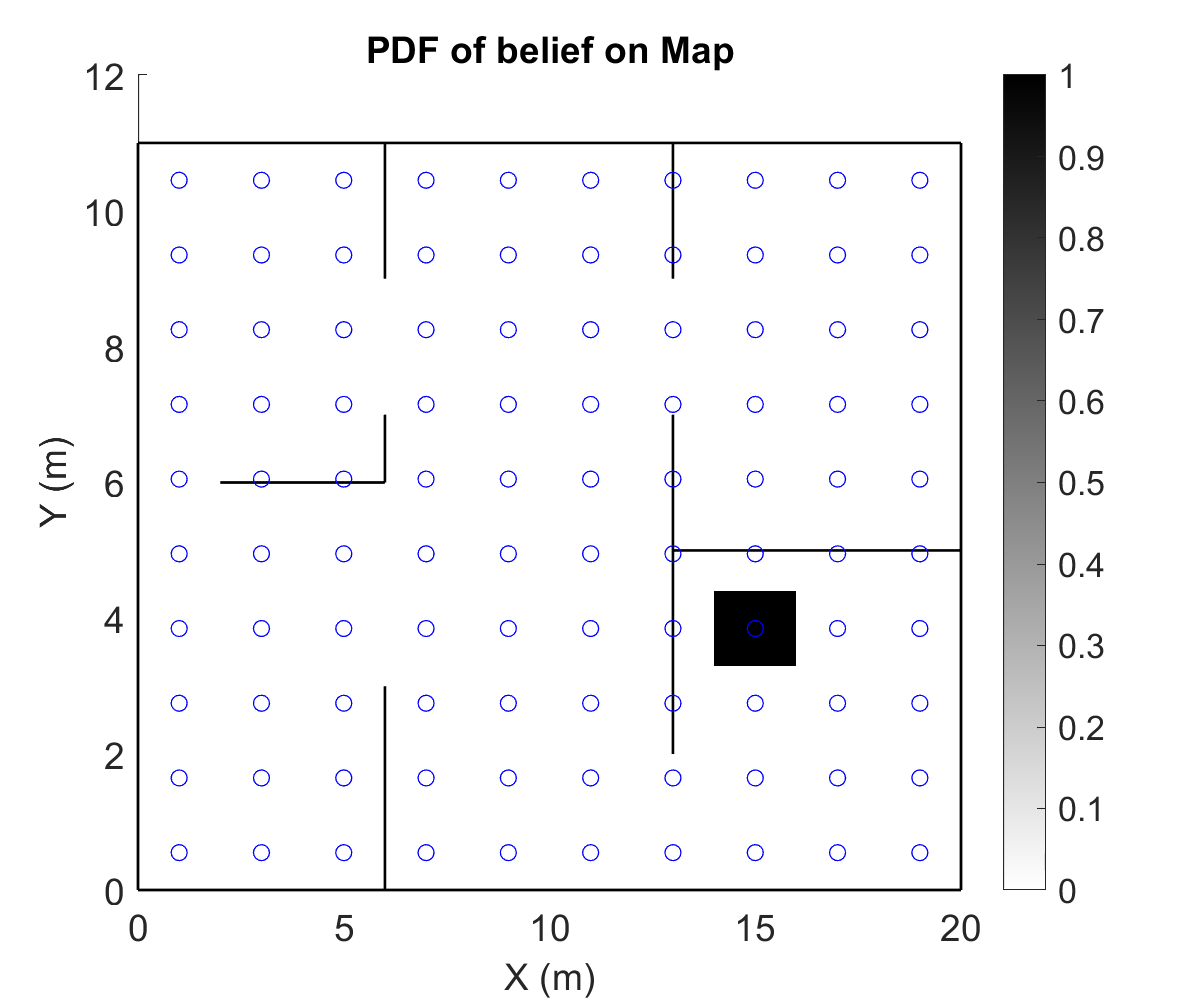
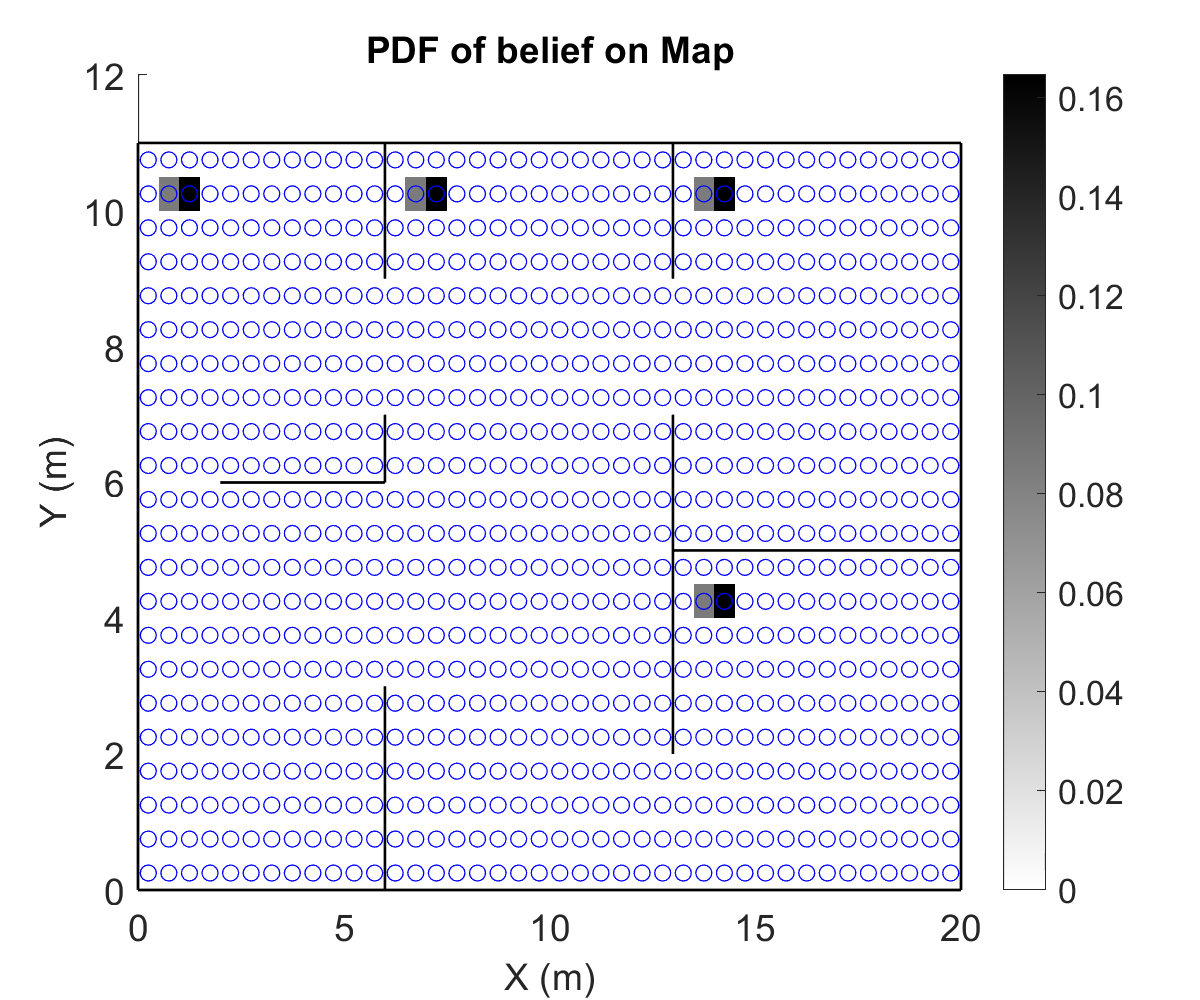
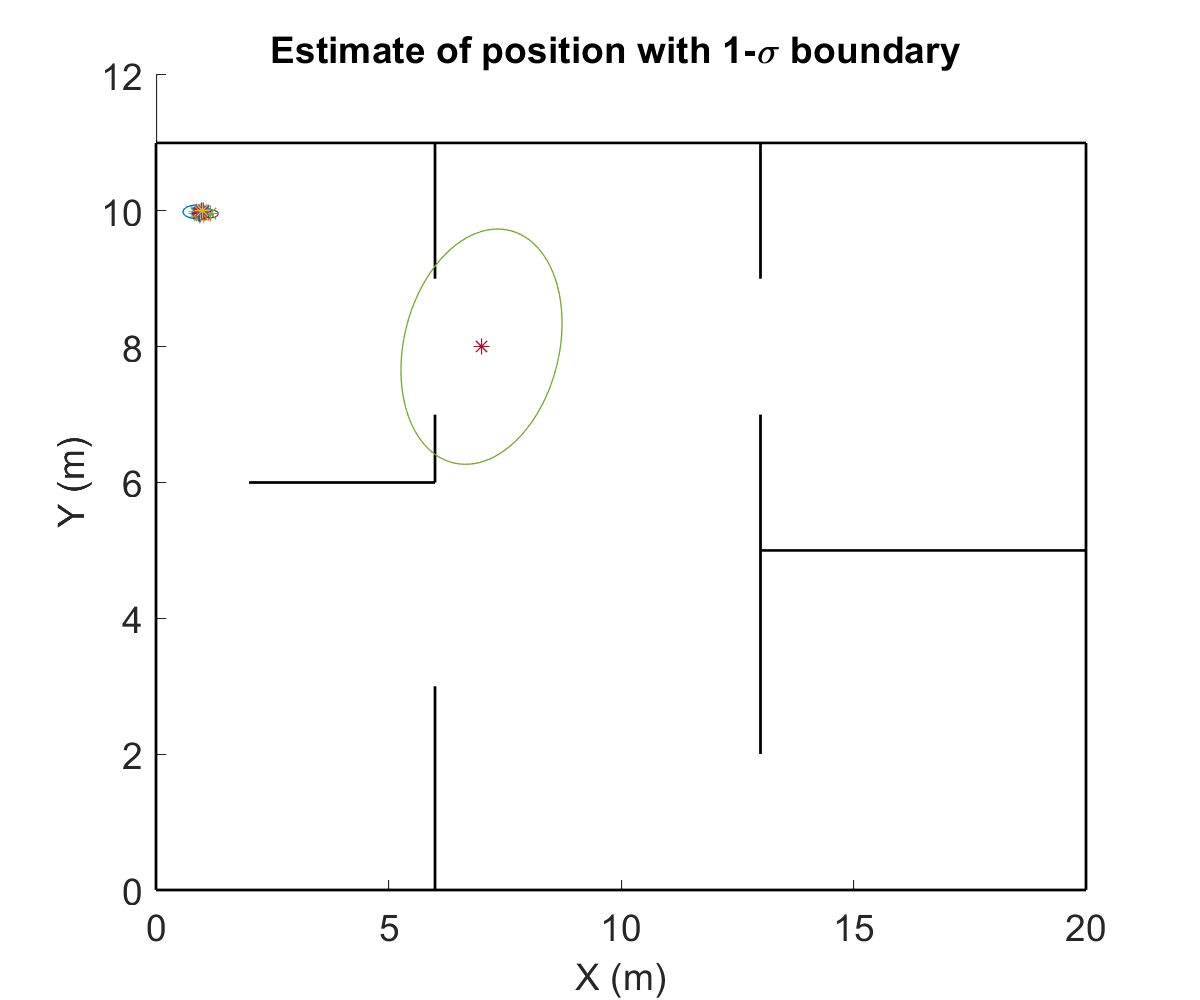
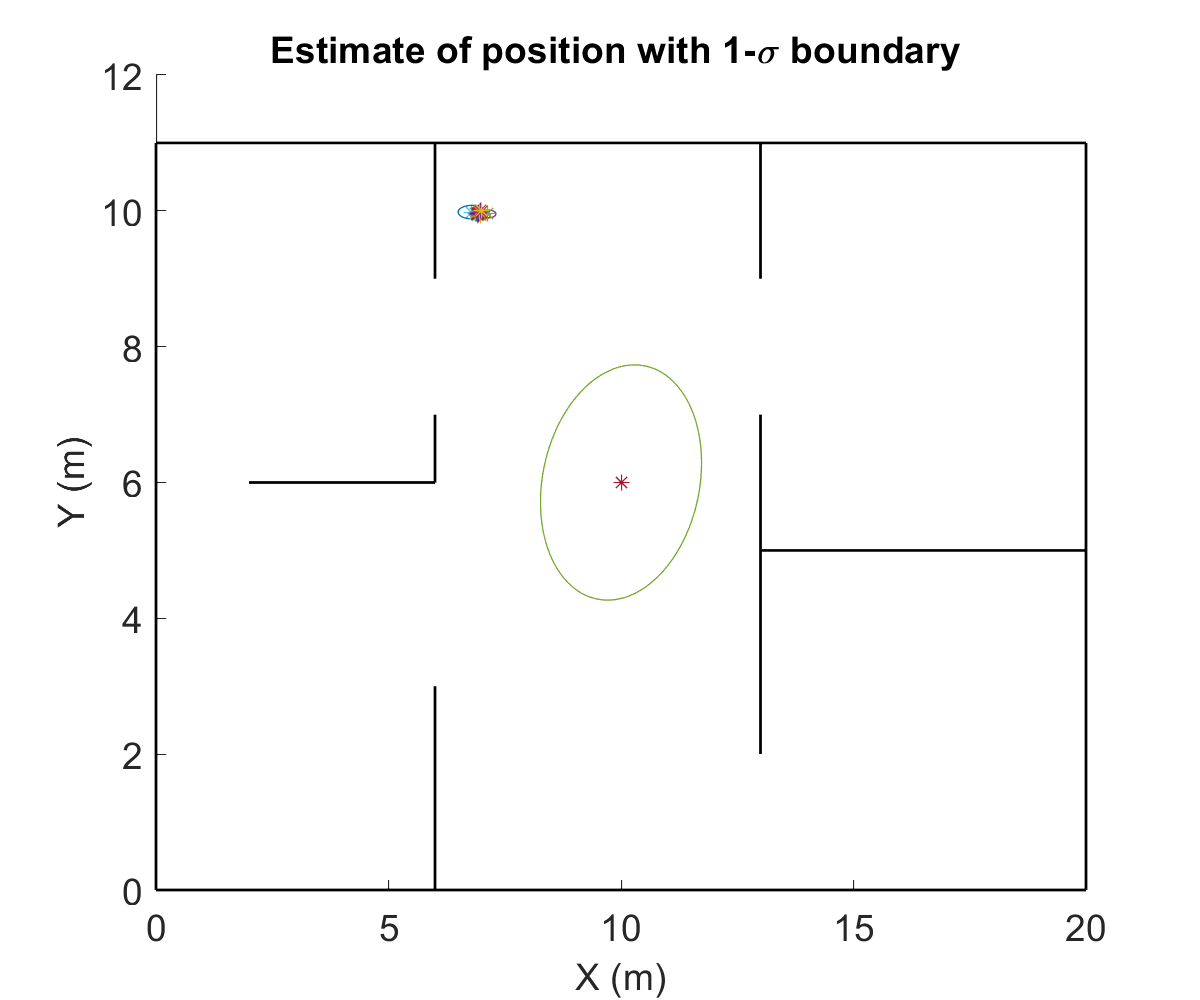
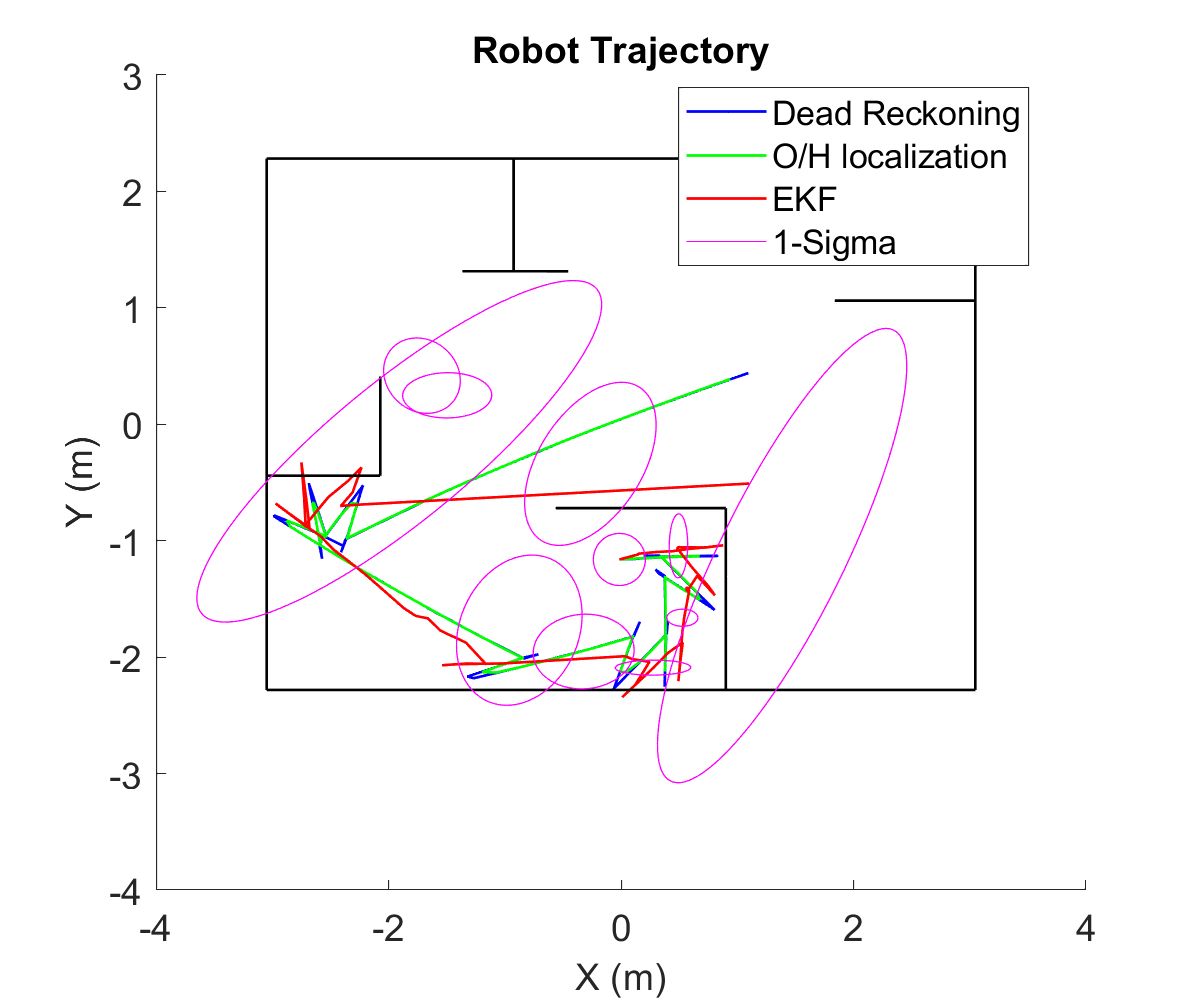
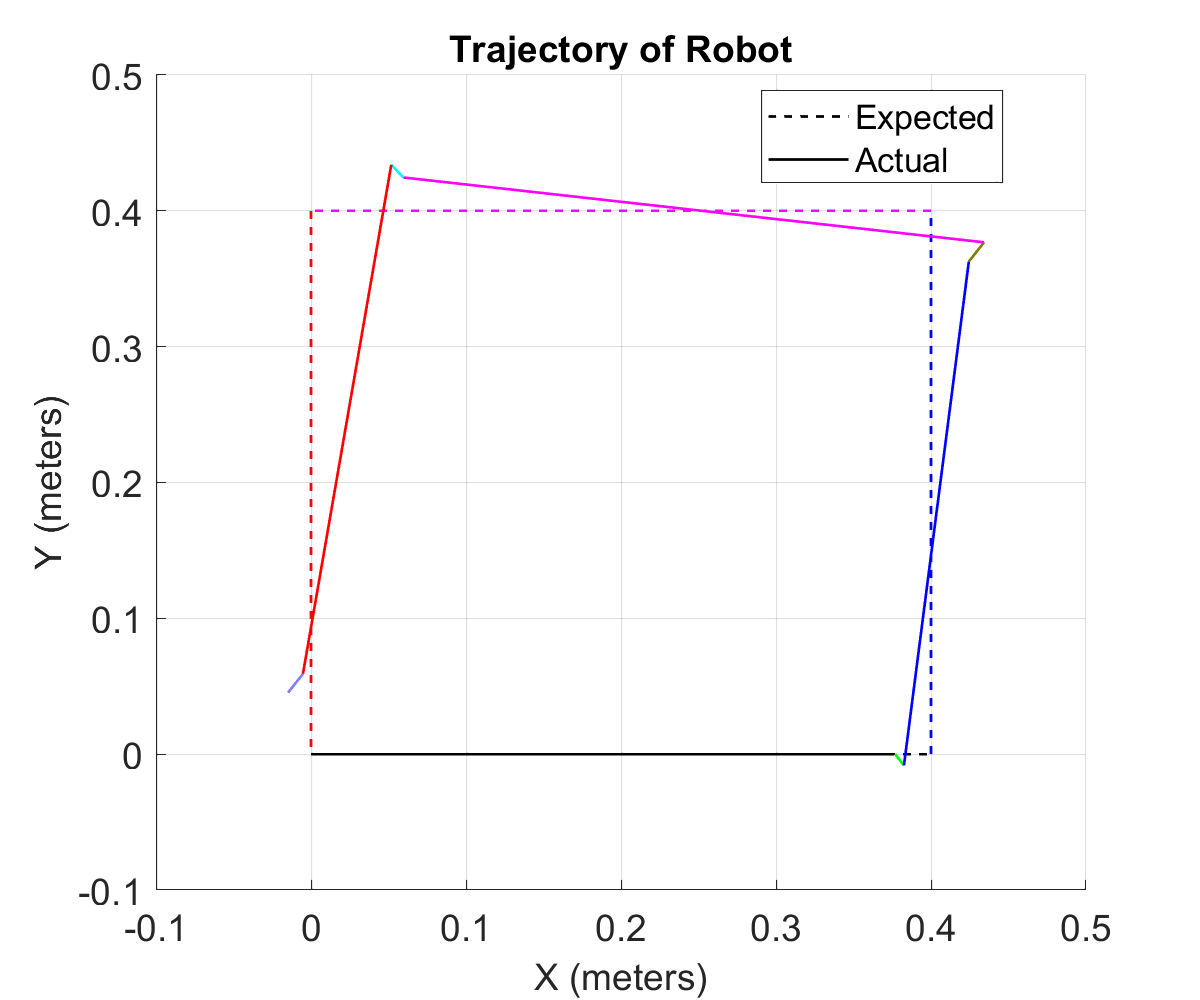
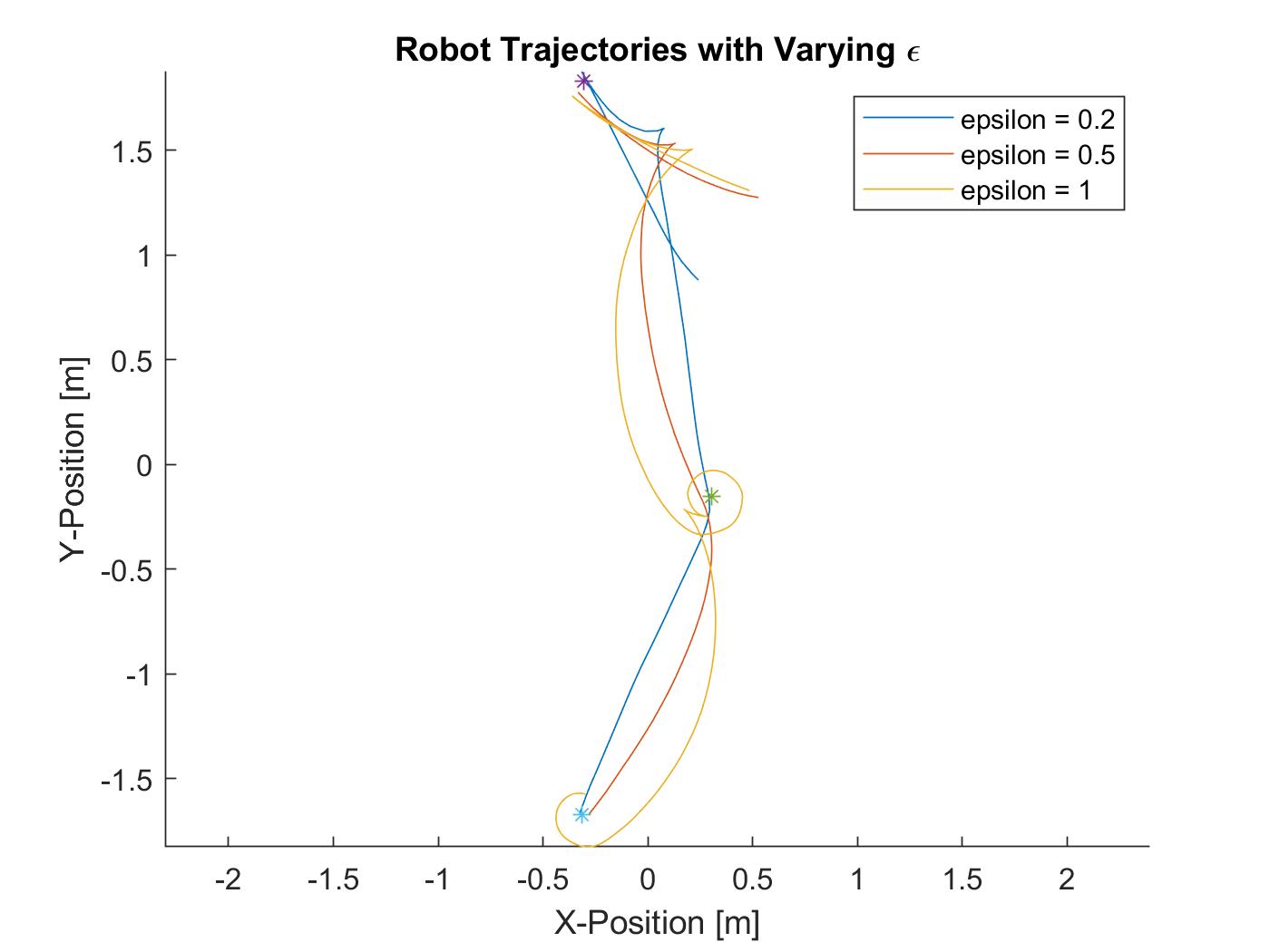
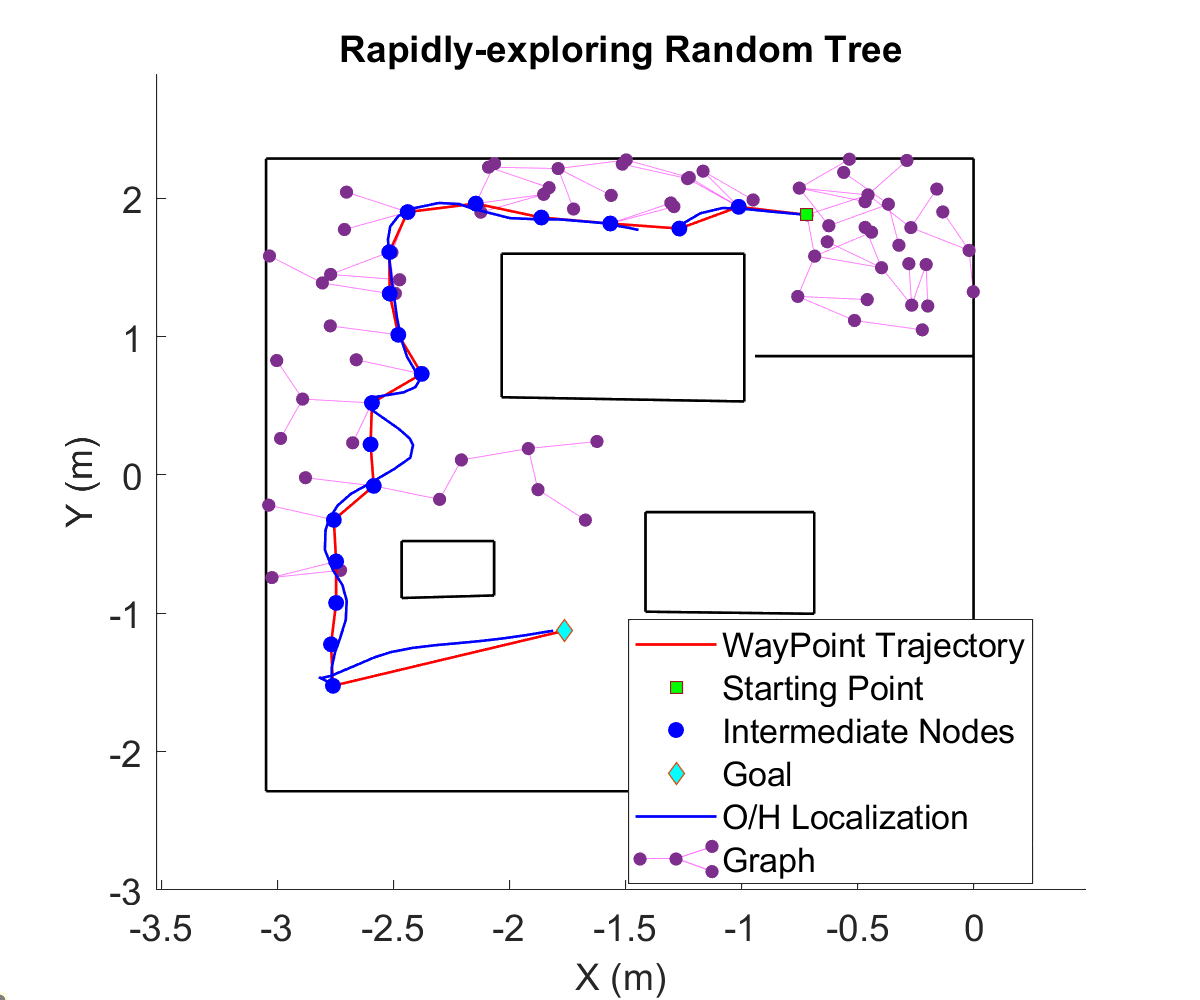
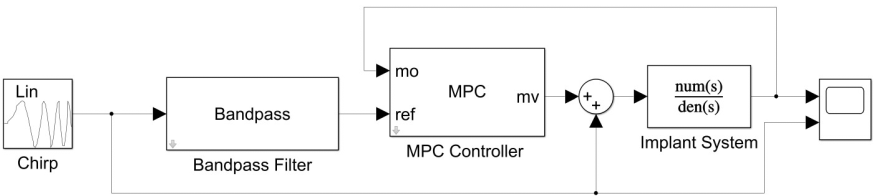
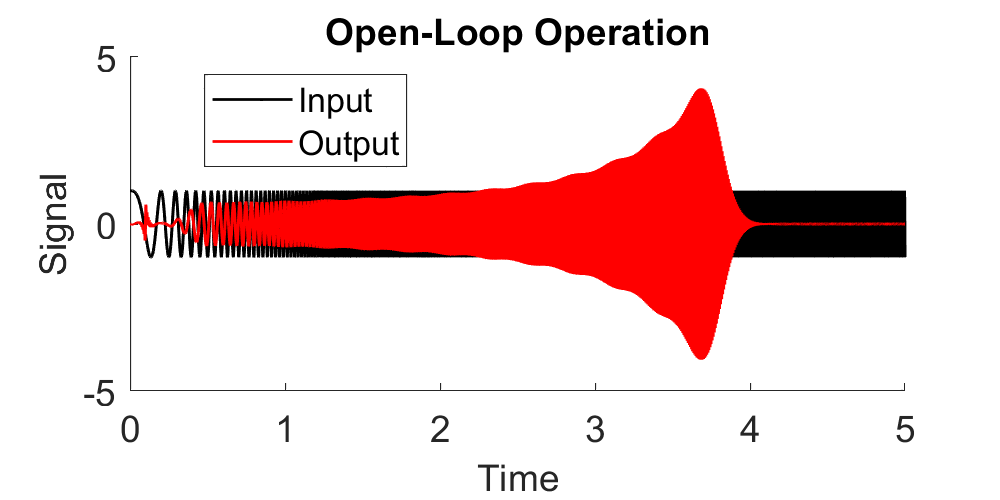
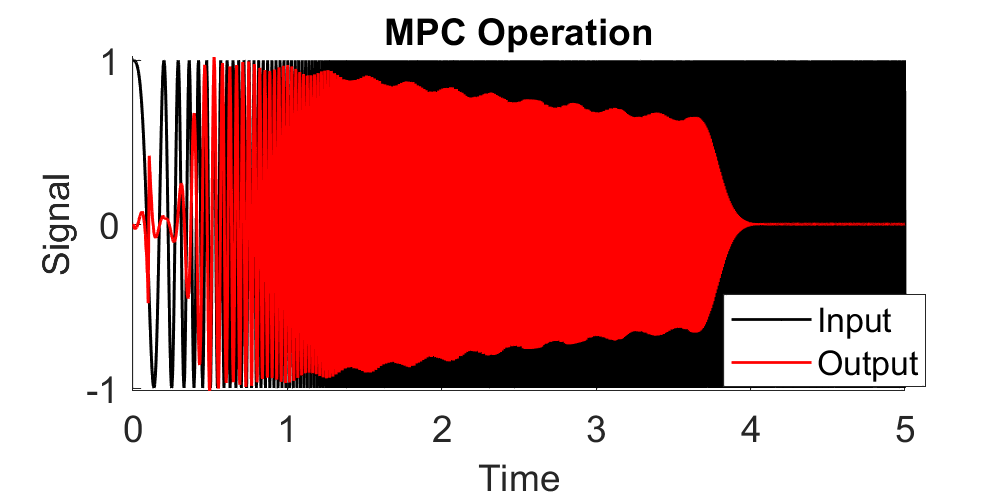
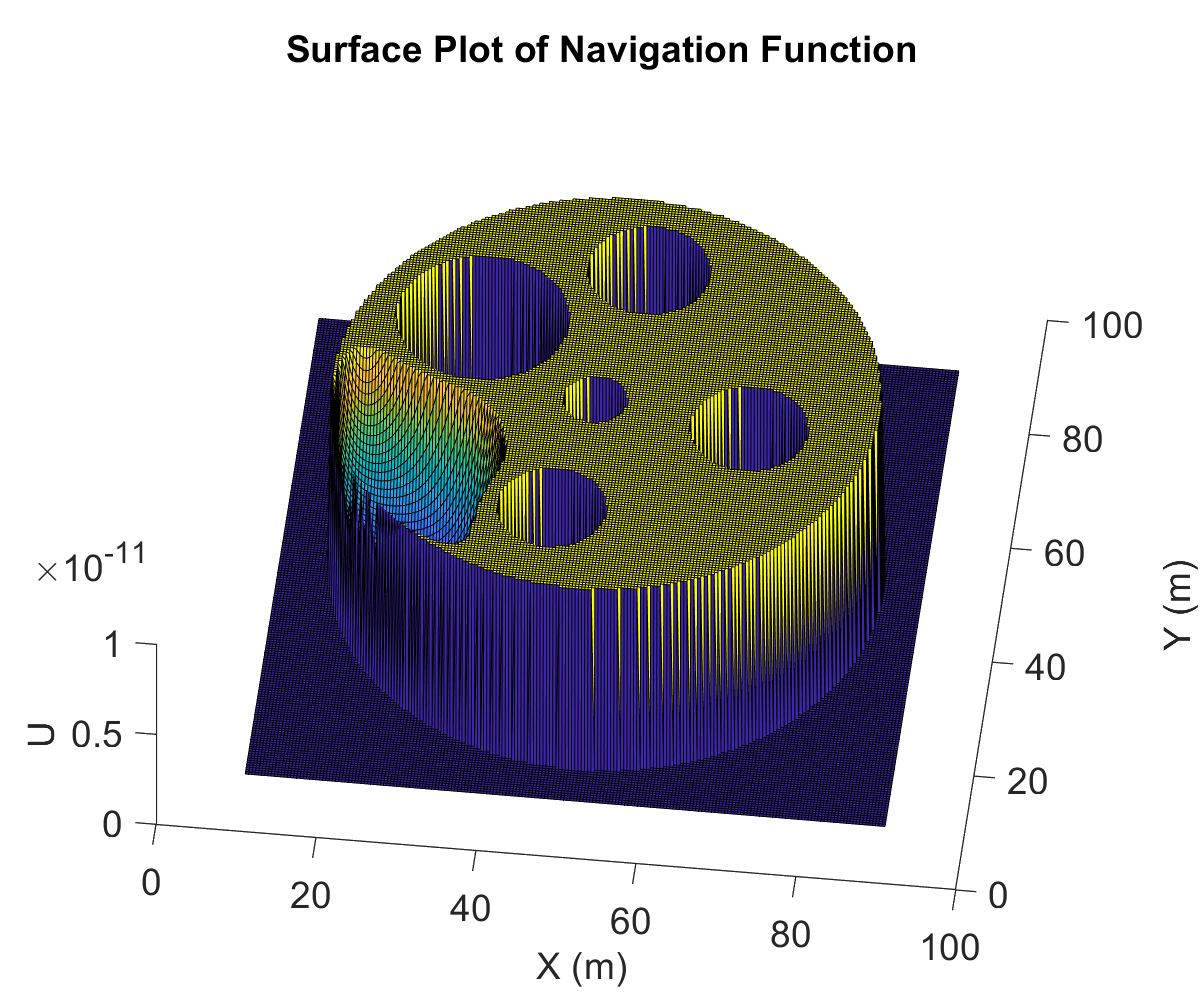
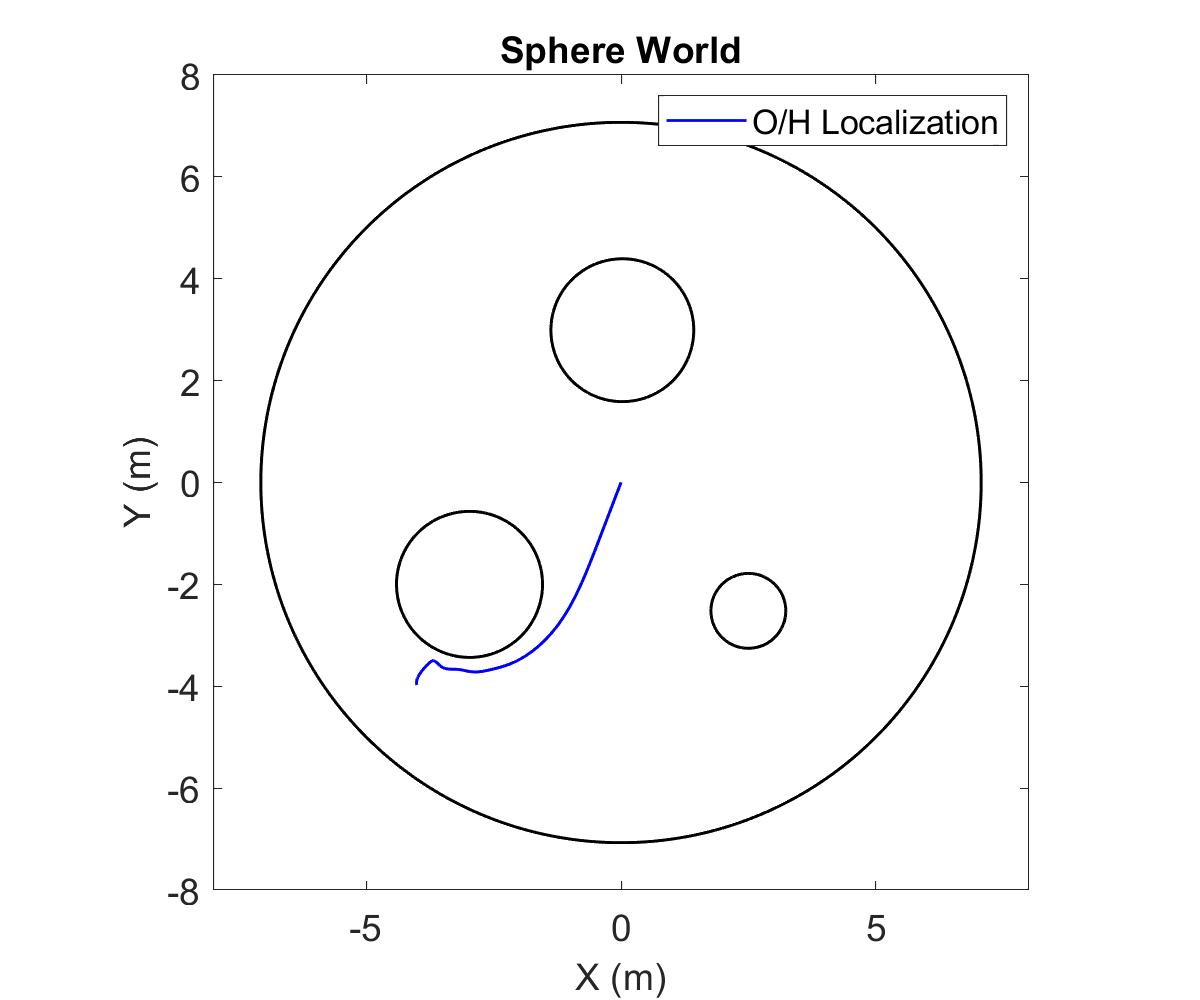
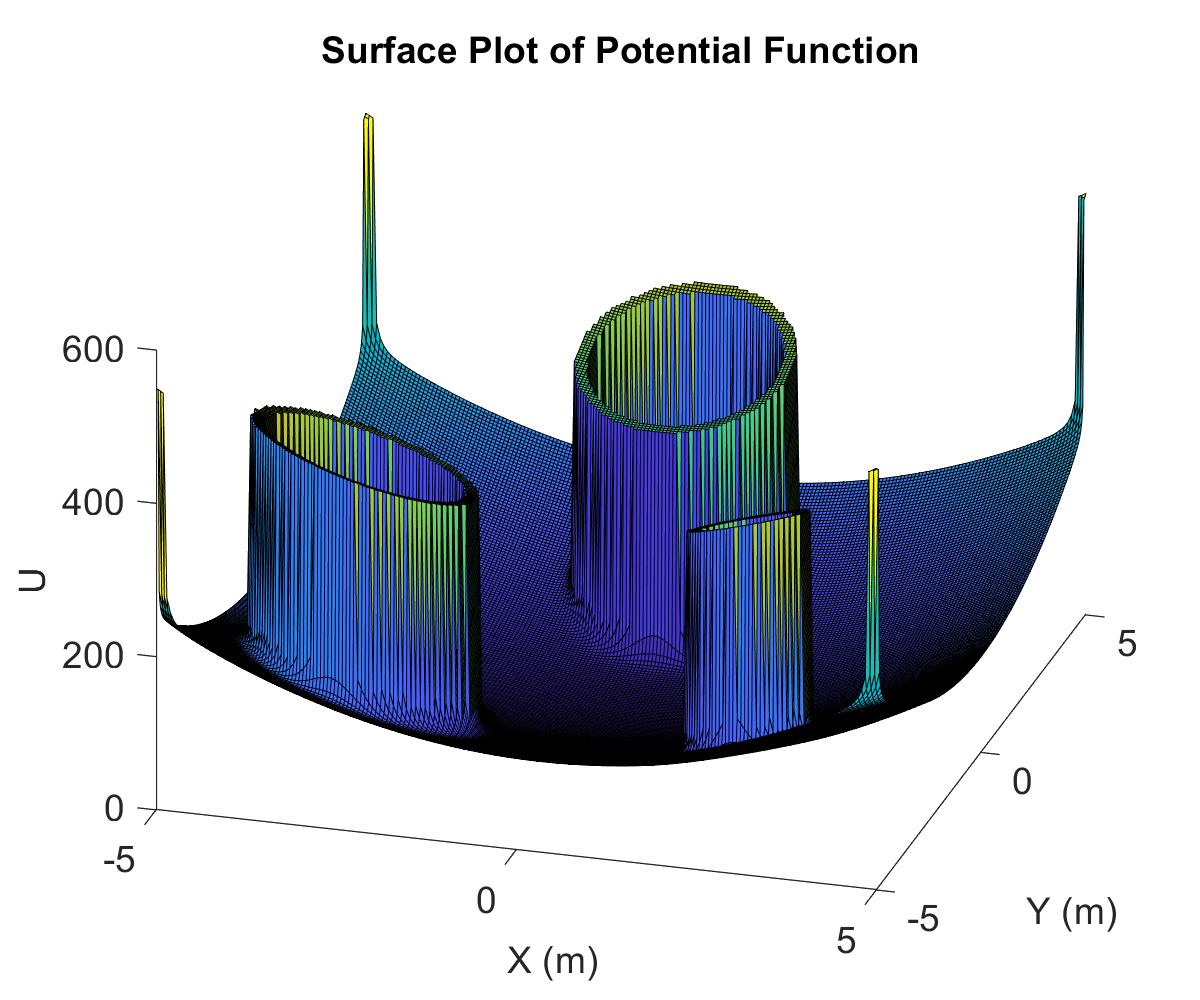
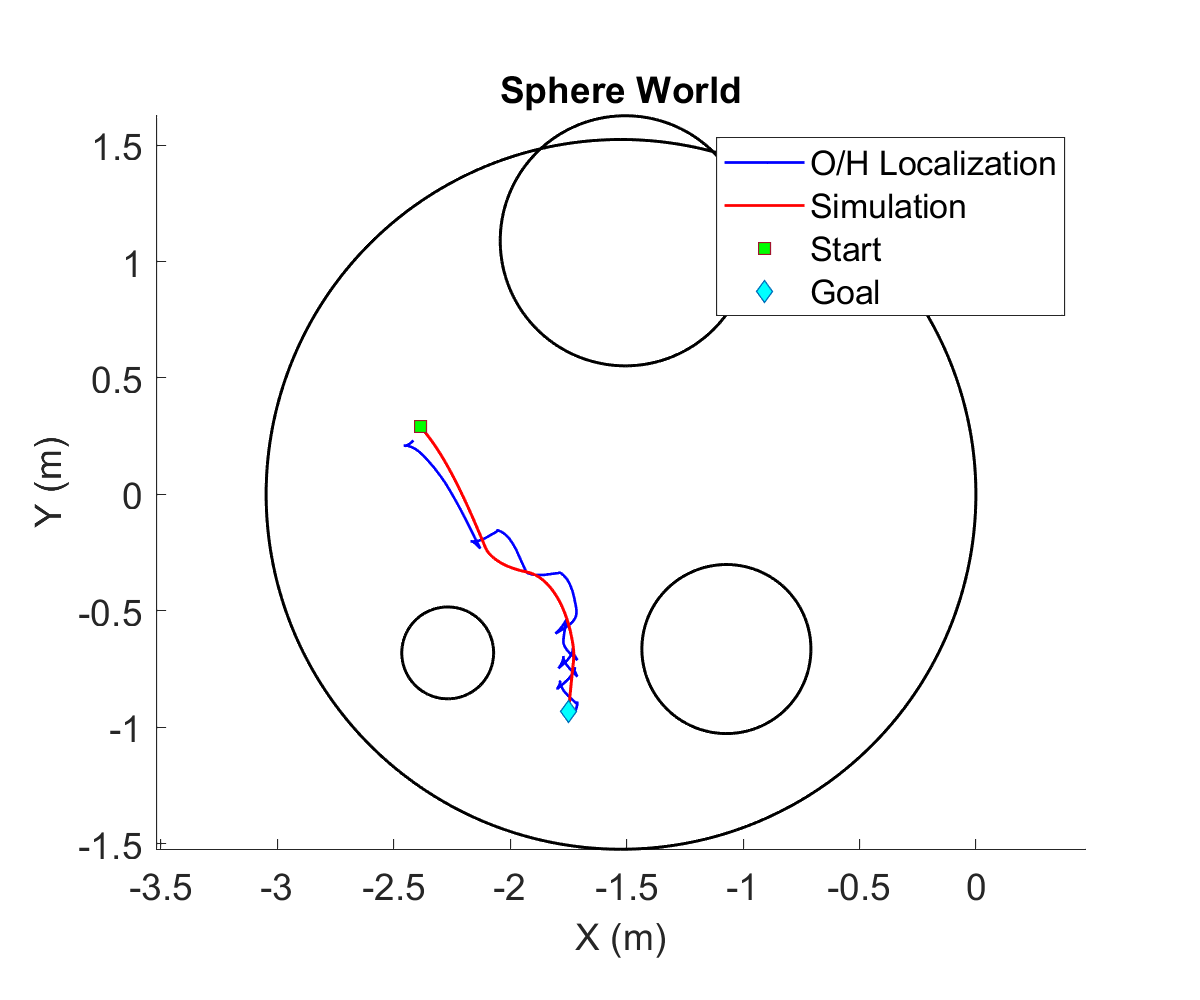
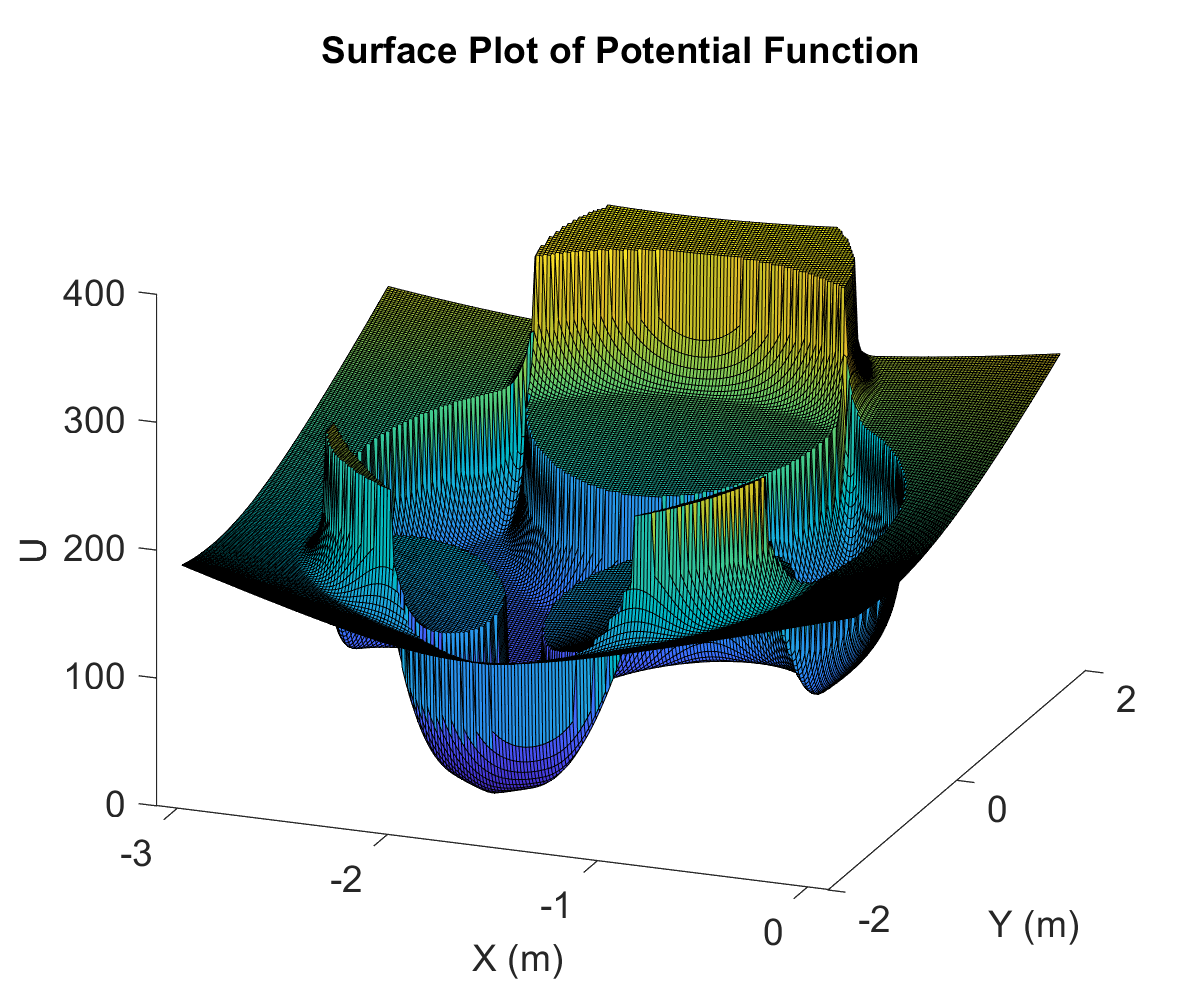
This project was a part of a larger umbrella-project of implenting motion planning algorithms. Probabilistic Roadmapping (PRM) are a set of algorithm which combine elements of both probabilistic reasoning and graph-based methods to generate feasible paths for a robot to navigate from a starting point to a goal point.

Github Link: https://github.com/pamraat/port-PRM
Notes: To operate this code, you'll need a valid MATLAB license and iRobotCreateSimulator toolbox which can be downloaded from here.

There are four PRM based methods implemented on the polygon environment shown in the figure below. Note that the PRM doesn't guarantee generation of a complete roadmap, and it significantly depends on complexity of the maps and number of sample points.

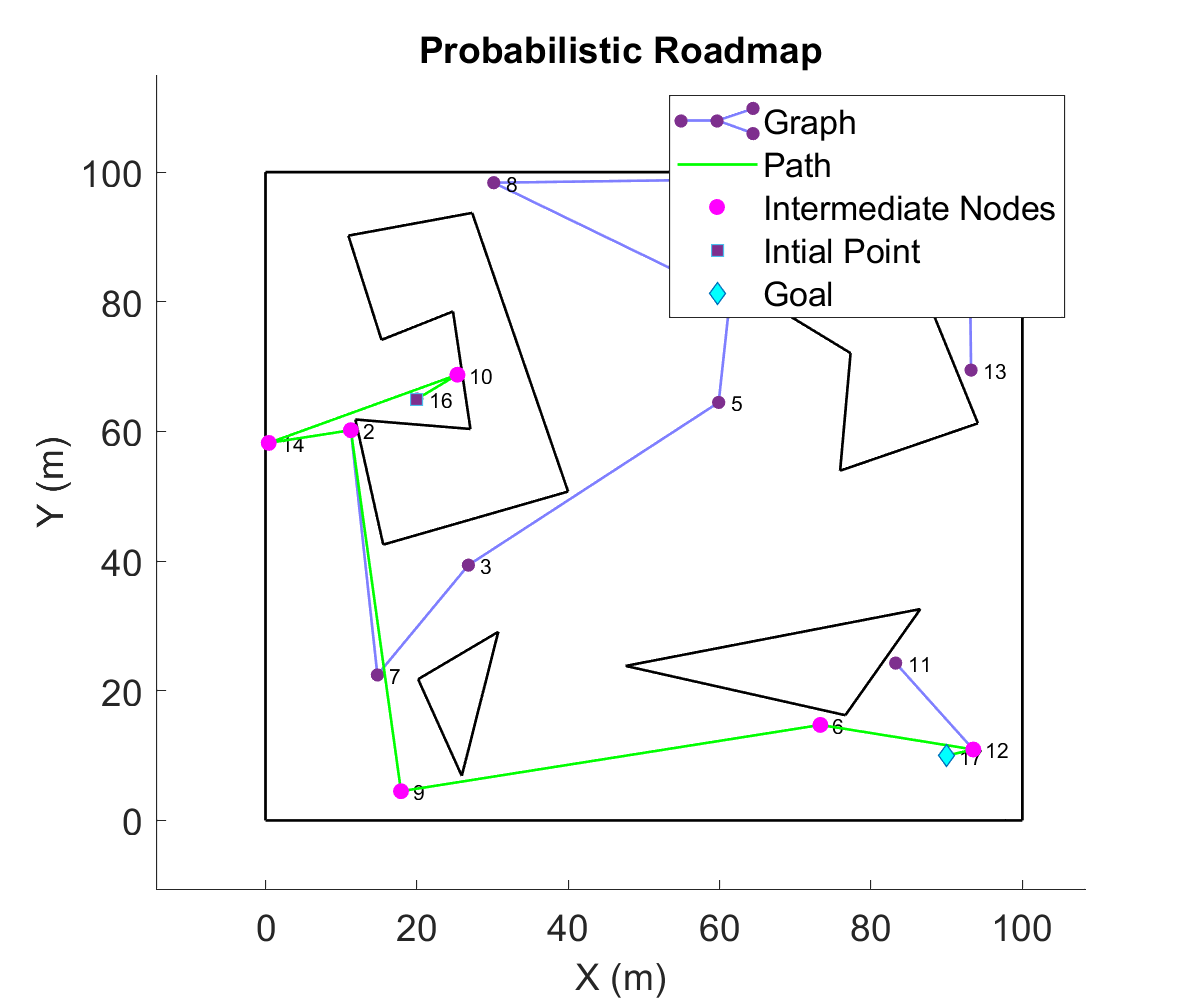
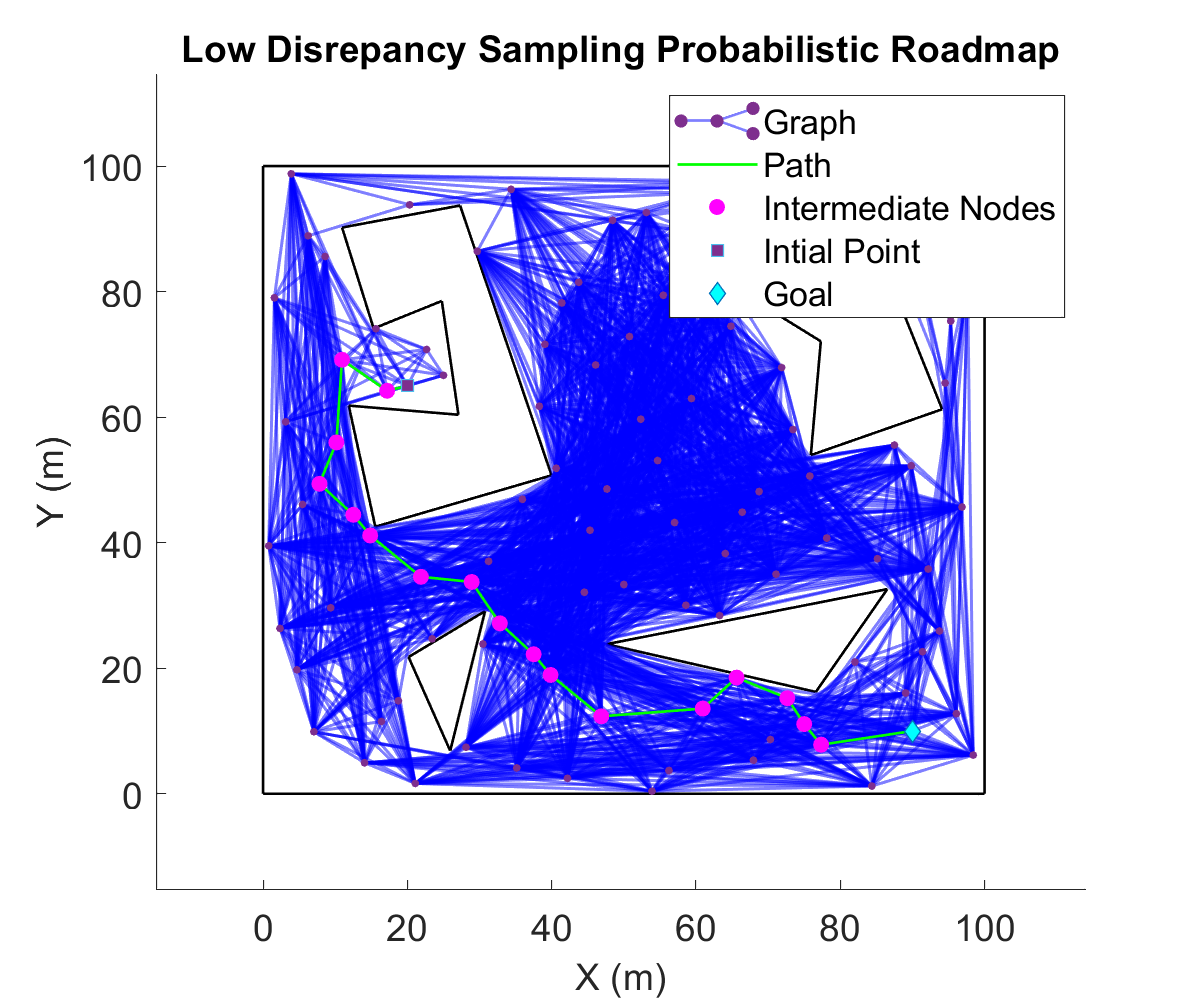
The figure below is a uniform sampling based PRM. In this, the points are randomly generated in free accessible space and the roadmap is generated by connecting each point to each point in line of sight. 50 points are sampled in the space. The figure below is a low discrepancy sampling based PRM. In this, the points are randomly generated in free accessible space, however, all the points belong to halton set, which mathematically spans space with lowest discrepancy. The roadmap is generated by connecting each point to each point in line of sight. 50 points are sampled in the space. 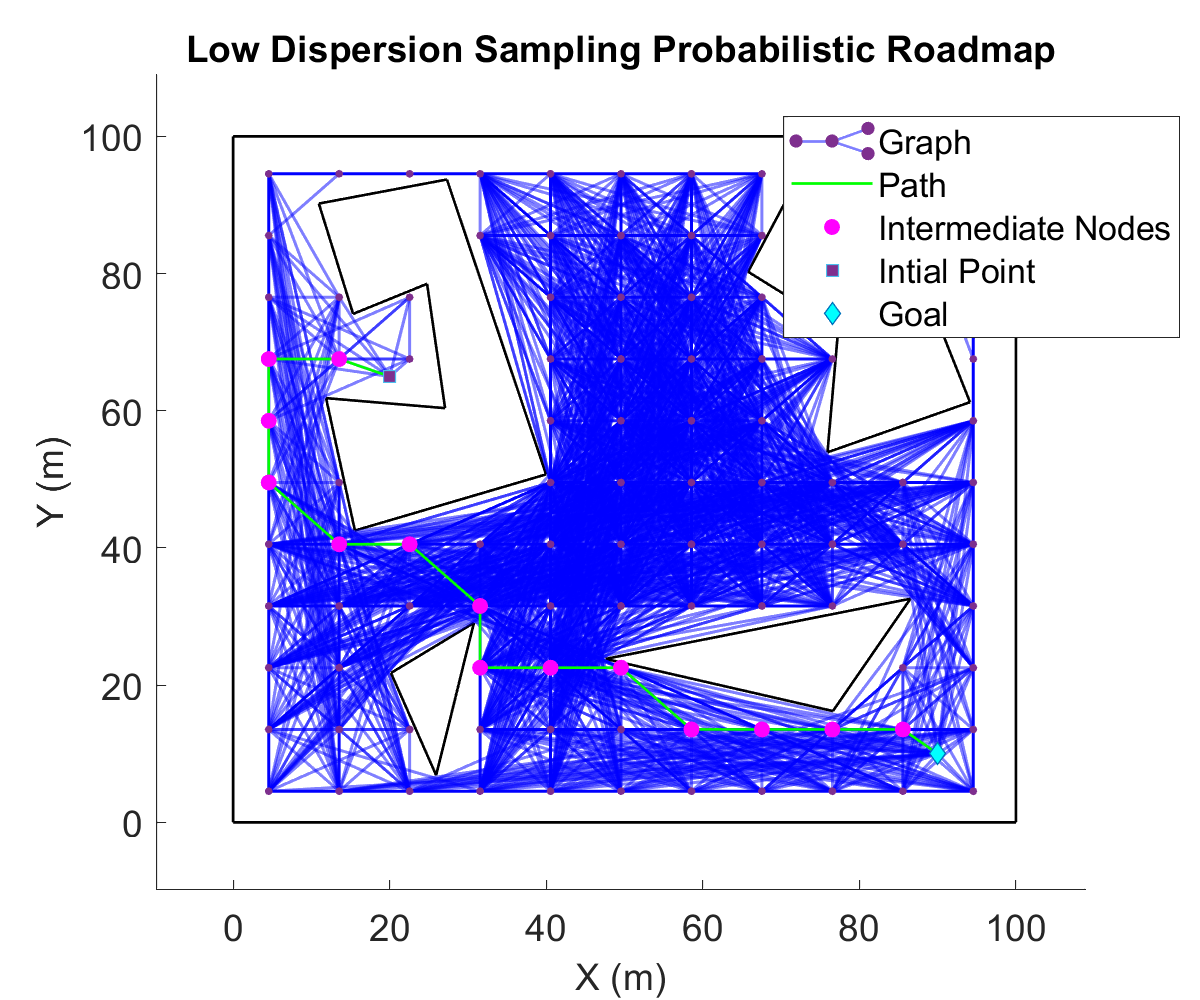The figure below is a low discrepancy sampling based PRM. In this, the points are randomly generated in free accessible space, however, all the points belong grid-like discretization, which mathematically spans space with lowest dispersion. The roadmap is generated by connecting each point to each point in line of sight. 50 points are sampled in the space. The figure below shows Visibility PRM. Instead of just randomly sampling in the free space, this algorithm considers the notion of visibility between sampled points. A new point is accepted if and only if the new points provides access to new region of free space which was inaccessible by already existing tree. This is extremely efficient roadmap, however computationally expensive.

This project was done to demonstrate the utility of Model Predictive Control (MPC) in adaptive and learning systems. The application of such systems spans wide range of engineering applications, from aircraft control to biomechanics.

Journal Paper link: https://doi.org/10.47852/bonviewJCCE3202768
Notes: To access this journal, you'll need a valid institutional or personal subscription to Journal of Cognitive and Computational engineering.

A digital twin of auditory system is created in Simulink. The system idenfication of this model is conducted using system idenfication toolbox of MATLAB. The transfer function is then used to build a system with MPC and intelligent feedforward system. The results of sound processing are then compared with standard open loop cochlear implants. The first following image shows the response of standard cochlear implants to 600 Hz to 1200 Hz chirp signal, and the second image represents MPC + feedfrward controlled response of cochlear implants.

This project was a part of a larger umbrella-project of implenting motion planning algorithms. Navigation functioms are mathematical representation of the environment such that the gradient of this representation always converge to the goal on the map.

Github Link: https://github.com/pamraat/port-roadmap
Notes: To operate this code, you'll need a valid MATLAB license and iRobotCreateSimulator toolbox which can be downloaded from here.

The limitation of such method is that the implementation on non circular geometries is excessively complicated. However, for the purpose of robot navigation, overestimation of objects' dimension is not a problem in most case, and an obstacle of anyshape can be represented by multiple overlapping circles to easily navigation functions around them. The following video shows robot control using navigation functions, where the squares are approximated as circles.

The trajectory plot of how robot perceived this environment is shown in the figure below. This map has associated navigation function as shown in figure below. Note that the high values of potentials around the wall push the robot towards sink, which is goal point at (0, 0). These codes used in the simulator were implemented on a real robot. The figure below shows the comparison of actual performance when compared to simulator. The actuation errors and actuation response time delays are the major reason behind the deviation. The potential function developed by the algorithm for the the real map is shown in the figure below.